最近の記事
インターネット・パソコン 
2016年10月 7日 (金)
2016年10月 6日 (木)
フラクタル図形の例: コッホ雪片
以前フラクタル図形を描画するアプリを紹介しました。
フラクタル(fractal)とは、フランスの数学者マンデルブロ (Mandelbrot) が導入した幾何学の概念で、図形の部分と全体が自己相似形になっているものなどをいいます。
海岸線や雲、山、樹木の枝分かれなどに見られる複雑な図形を数学的に理論化しました。
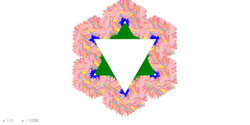
ここでは、前記アプリで作成したフラクタル図形のうち、コッホ雪片の例を示します。
(コッホ雪片を選択、重ね描きをOn、初期表示色をgreen、線の太さ:50)
2016年9月22日 (木)
PCで突然キー入力ができなくなった!
昨日(9/21)夕方、PC(NEC LAVIE NS750)で種々作業中にキー入力が突然できなくなりました。
そこで、「スタート」->「電源」->「再起動」をクリックして、PCの再起動を試みましたが、画面中央に「再起動しています」のメッセージが出たところから一向に次に進みません。
当然「Ctrl+Alt+Del」での強制終了もできず、また電源ボタンを長押ししてもOffになりません。
販売店(Edion)の担当者にTELし、対処法を教わりました。
-> 電源コードを抜いて、バッテリーがなくなるまで待つ(本機はバッテリーの取り外し不可)
(注)バッテリーの取り外しができれば簡単なのだが・・・。
カタログによれば本機のバッテリー駆動時間は約4.3H。
ところが18時に電源コードを抜いて待つこと5時間、23時になってもOffになりません。
翌朝起きて確認してもまだOnのままです。
漸く7:50頃にOffになりました。 約14時間かかりました。
この間ディスクも動いておらず、あまり電力を消費しなかったために長時間を要したようです。
電源コードを差し込み、PCの電源ボタンを押して、復旧しました。
起動後、PCの動きが重いのでタスクマネージャで確認すると、「Windows問題レポート」なるプロセスが走っていたので、強制終了させました。
2016年8月21日 (日)
フラクタル図形を描くアプリ
フラクタル(fractal)とは、フランスの数学者マンデルブロ (Mandelbrot) が導入した幾何学の概念で、図形の部分と全体が自己相似形になっているものなどをいいます。
海岸線や雲、山、樹木の枝分かれなどに見られる複雑な図形を数学的に理論化しました。
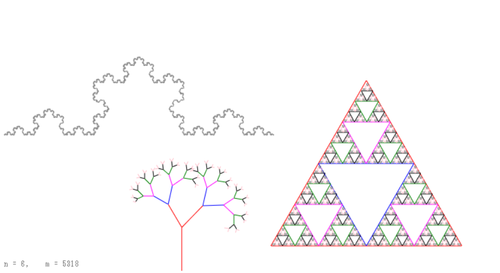
下記の代表的なフラクタル図形を描くアプリを紹介します。
(1)コッホ曲線(Koch curve)
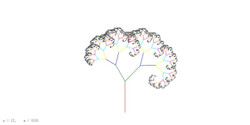
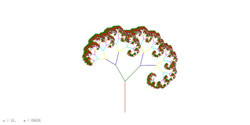
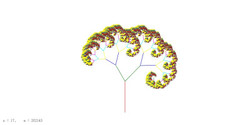
(2)2進木(Binary tree)
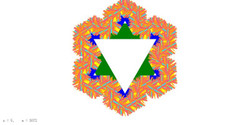
(3)シェルピンスキーのガスケット(Sierpinski's gasket)
2016年3月 2日 (水)
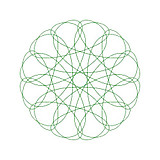
点列を滑らかに結ぶアプリ
任意に入力された点列や各種パターン状の点列を滑らかに結ぶアプリを紹介します。
本Blogで以前、
・正5角形とその仲間たち
・星形多角形をもとに作成した花模様
・正100角形をもとに作成した模様の例
・風車から花模様を
と題して紹介した色々な模様は下記アプリで作成したものです。
-> 自由曲線の描画アプリ
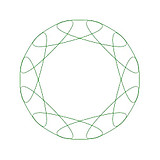
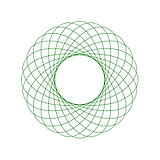
このアプリでは次のようなものも作成できます。
2016年2月 9日 (火)
風車から花模様を
10枚の羽根からなる風車の形状(左上の図)をもとに、各頂点(全部で40点)を順に滑らかに結んで得られる曲線の数々はまるで花びらのようです。
これらの模様は任意に入力された点列や各種パターン状の点列を滑らかに結ぶ下記アプリで作成できます。
-> 自由曲線の描画アプリ
2016年2月 7日 (日)
2016年2月 5日 (金)
正100角形をもとに作成した模様の例
正100角形をもとに、その頂点を順に滑らかに結んだ自由曲線の接線ベクトルの長さを変化させるときれいな模様が得られます。
その1例を示します。 (右下の図形は左下の図形の中心部を拡大したもの)
上記の色々な模様は下記アプリで作成したものです。
-> 自由曲線の描画アプリ
2016年2月 3日 (水)
星形多角形をもとに作成した花模様
星形多角形には種々のものがありますが、ここでは正12/5角形をベースに作成したいくつかの花模様を紹介します。
すべて左上の図形(正12/5角形)の12個の頂点を通る曲線です(但し、スケーリングしている)。
上記の色々な模様は下記アプリで作成したものです。
-> 自由曲線の描画アプリ
2016年2月 1日 (月)
正5角形とその仲間たち
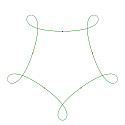
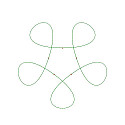
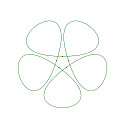
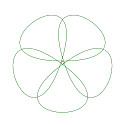
正5角形をもとに、その5頂点を滑らかな曲線で結んだ自由曲線、更にその曲線の接線ベクトルの長さを変化させて得られる様々な曲線の例を示します。
以下の図形は、正5角形の各辺の中点を加えた10点を滑らかに結び、その曲線の接線ベクトルの長さを変化させて得られる様々な曲線たちです。
上記の色々な模様は下記アプリで作成したものです。
-> 自由曲線の描画アプリ