■ 自由曲線の描画（JavaScript版）

　マウス入力またはパターン入力された点群を結ぶ滑らかな曲線（自由曲線）を生成し、表示します。
　入力点（通過点）での接線ベクトルの長さを変化させると様々な形状が得られます。

　・入力された点は点列の最後に追加される。
　・点の挿入：　「点の挿入」ボタン－＞挿入個所を指示－＞点を入力（指示点の前に挿入される）。
　　　　　　　　　挿入モード時に再度「点の挿入」ボタンを押すとキャンセルされる。
　・点の削除：　マウス右クリックで削除する点を指示する。
　・点の移動：　移動したい点をドラッグ＆ドロップする。
　・アニメーション表示：　始点から終点に向けて描画する様子を表示する。
　その他の機能については後述。
　（注）本アプリは現在改良中であり、仕様が変わる可能性あり。

---

図形の形状：	開図形	閉図形	パターン図形入力：
表示方法：	折れ線	曲線	線の太さ：	壁紙：
色の指定：	主図形	点番号・マーク	接線ベクトル	制御点マーク	3点を通る円
端点での接線ﾍﾞｸﾄﾙ計算法：	単純（弦方向）	FMILL方式	円弧法
接線ﾍﾞｸﾄﾙの長さ（対弦長比）：
点の挿入・削除：
図形の座標変換：
各種 option指定：	点番号表示	点マーク表示	制御点表示	grid表示	grid入力
	座標系表示	3点を通る円表示		ホイール有効	点削除時の確認
アニメーション表示：		ステップ実行		線の色：	線の太さ：

数値データ：

save用画像

---

その他の機能：

・パターン図形入力
　・正多角形（３～１２角形、任意の正多角形）
　　　多角形は外径と繰返し数（分割数）を指定
　・星形多角形は外径を」指定
　・歯車（花びら）：枚数とタイプ（0-5）、外径 [,内径] を指定。内径省略時は外径の4/5
　・ランダム点列入力（タイプ 0-3）
　・その他登録図形あり
　・パターン入力された図形も編集（点の削除・移動・追加）可能

・各部の色指定可
　　主図形（形状線）は多色指定できる
・接線ベクトルの長さ（弦長に対する比）を変更できる
　　直接指定、現在値に対する増減比率指定可能
　　接線ベクトルの長さをマイナスにすると、面白い図形が得られる
・端点での接線ベクトル：　開曲線に対して3種類の計算方法を選択可
　　任意の接線ベクトル（制御点）も指定可能
・grid入力 ON時、入力点は最も近いグリッド点に丸められる（但し、grid表示時に有効）
・壁紙（背景画像）指定可能
　　明るさ（濃淡）を変えることができる
　　ネガ反転、モノクロ変換、エッジ検出（風景画風）も可能
・「アフィン」（アフィン変換、2次元）
　　次式で表現される座標変換である。 係数 a1,a2, .., b3 を入力する
　　　X = a₁x + a₂y + a₃
　　　Y = b₁x + b₂y + b₃
　　アフィン変換の例：　拡大縮小、回転、ミラー、スキュー（せん断）、…
　　簡易入力： 0 ー＞menu表示
・「ランダム」で入力点をランダムに移動する
・拡大縮小はmouseWheelでもOK（有効/無効の切替あり）
・アニメによる一筆書き描画： ステップ実行、スピード変更可
・表示された図形をファイルに出力するには
　　「save」ボタンでイメージデータに変換
　　　　－＞ 変換表示された画面上で右クリックしてコピー　－＞ ペイントに貼り付け　－＞ 出力

　与えられた点列を通る滑らかな曲線が自由曲線で、色々な方式がある。
　ここでは、ベジェ（Bézier）曲線を取り上げる。


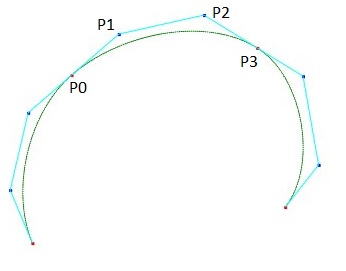
　図の自由曲線は4個の通過点を結ぶ3個のセグメント（部分曲線）から構成されている。
　中央のセグメントの両端点をP0、P3、制御点をP1、P2 とするとき、この部分のベジェ曲線は次式で定義される。
　　P = P0・(1-t)³ + P1・3t(1-t)² + P2・3t²(1-t) + P3・t³
　　ここで、0 ≦ t ≦ 1
　ベクトルP0P1、P3P2 はそれぞれ端点P0、P3での接線ベクトルであり、例えば点P3の右側のセグメントに対する接線ベクトルは図のようにベクトルP3P2と逆向きになるように決定する。
　これにより、各セグメントは滑らかに接続される。