★ 参考までに、本アプリで使用している計算式とその誘導過程を示す。
● 踏込時間を無視した場合
● 踏込時間内の減速を考慮した場合[ 停止距離の計算式 ] ・速度をv0 (m/s)、 摩擦係数をμ、反応時間をta (s)、重力加速度をg (m/s2) とする。 ・空走時間 t0 = ta 空走距離 d0 = v0・t0 ・制動時間 t1 = v0/(μg) 制動距離 d1 = v02/(2μg) ・・・(踏込時間内の減速については別途考慮) ・停止時間 t2 = t0 + t1 停止距離 d2 = d0 + d1 [ 制動時間・制動距離の計算式の誘導 ] ・車の質量をm(kg)とし、進行方向にX軸をとって時刻t(s)における車の位置をx(m)とする。 ・次の運動方程式が成立する。 mx" = -μmg ここで、" は位置xの時刻tに関する2回微分(加速度) ・これを解くと、 x" = -μg x' = -μgt + v0 x = -μgt2/2 + v0・t ・制動時間 t1は x'(速度)= 0 より、 t1 = v0/(μg) ・制動距離 d1はこのt1をxの式に代入して、 d1 = -μg[v0/(μg)]2/2 + v0・v0/(μg) = v02/(2μg) 尚、この式は車の運動エネルギー(mv02/2)が摩擦力による仕事(μmg・d1)に変換されることから、 mv02/2 = μmg・d1 より求めることもできる。
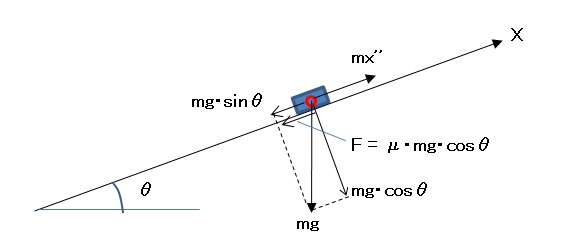
・ブレーキの踏込時間tf内に減速度が直線的に増加して、主制動時間内の減速度(μg=一定)に達すると仮定すると、 踏込時間内の速度低下量Δvは減速度線図(緑色)の3角形部分の面積より、 Δv = μg・tf /2 ・踏込開始時からの時間経過をtとすると、時刻 t における速度 v は v = v0 - Δv・(t / tf)2 ・従って、この間の走行距離:df は df = ∫0tf v dt = v0・tf - Δv・tf /3 ・次に、減速度一定(=μg)区間の走行距離:dm は、区間開始時の速度が (v0 - Δv) であることから、 dm = (v0 - Δv)2/(2μg) ・以上により、踏込時間を考慮した制動距離は d1f = df + dm● 坂道(斜面)での制動時間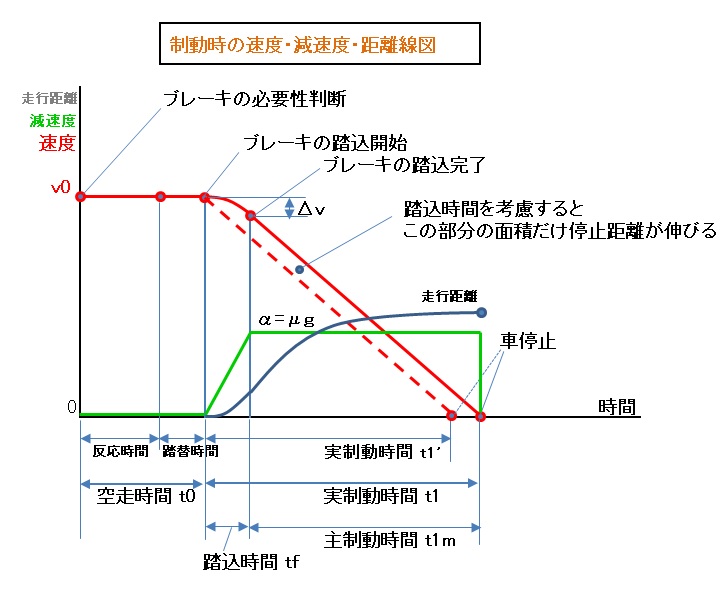
上り坂(θ> 0)や下り坂(θ< 0)における車の制動距離について考える。 ・次の運動方程式が成立する。 mx" = -μmg・cosθ - mg・sinθ = -(μ・cosθ + sinθ)・mg ・この式は、平坦な道路上の運動方程式(mx" = -μmg)における摩擦係数μを μ -> μ' = μ・cosθ + sinθ に変更したもである。 ・従って、坂道での制動計算は傾斜角θを本来の摩擦係数μに加味した「μ'」を使用することで行うことができる。 ・又、重力の斜面方向の分力と摩擦力の関係から、 μ” = μ・cosθ - sinθ の値が負になる場合: ・上り坂では 一旦停止する(速度0になる)が、その後下方に滑り落ちる。 ・下り坂では 停止できない(速度0にならない)