■ 太陽光発電： 自動追従システム再考(4)　～ 任意軸周り自動追従方式 ～ （JavaScript版）

　以前、発電パネルを太陽の方向に自動追従（追尾）させる次の２方式の発電量について、パネル固定方式と比較して表示するアプリを紹介しました。

（１）水平面内自動追従方式　（水平面内旋回のみ、首振りなし）
　　　　パネルの方位角のみを太陽の方向に追従させる。
（２）完全自動追従方式　　　　（水平面内旋回 ＋ 上下首振り）
　　　　パネルの傾斜角、方位角を太陽の方向に追従させる（パネル面 ⊥ 太陽光）。

　ここでは、任意の１軸周りにパネルを自動旋回させて受光日射量を最大（従って発電量を最大）にする方式について検討し、それに基づくシミュレーションプログラムを作成したので紹介します。　本方式の基本計算式は後述のとおりです。

　太陽光発電システムの発電量を推定するために必要な斜面日射量は水平面全天日射量の観測値からErbsモデルにより算出しています。
　発電量は斜面日射量に比例するので、斜面日射量の比が発電量の比となります。

＜ 対象地点 ＞
　　次の15府県を除く32の都道府県庁所在地。
　　　茨城県、千葉県、埼玉県、神奈川県、石川県、岐阜県、滋賀県、三重県
　　　京都府、和歌山県、兵庫県、岡山県、鳥取県、山口県、徳島県

＜ 対象期間 ＞
　　2013年1月　～　12月

＜ 使い方の説明 ＞
　・地点、月日、屋根傾斜角、方位角を指定する。
　　　方位は真南が0度、東が-90度、西が+90度。
　・「計算＆ｸﾞﾗﾌ描画」ボタンを押すと、各時間毎の斜面日射量が計算され、表示される。
　　　固定方式に対する追従方式の1日の日射量比（＝発電量比）が最後に表示される。
　・月毎の比較、年間の比較
　　　表の右上の「日」の欄をクリックする。
　　　すると、固定方式に対する自動追従方式の日射量の比（発電量の比）の算出期間を、
　　　　日（指定日）　－＞　月（指定日の属する月）　－＞　年（2013年）
　　　の順で切替えることができる（1番右側の％の欄のみ。その他は指定日の値）。
　・任意軸周り自動追従方式の回転軸ベクトルの指定方法
　　　対象地点を原点、西方向をX軸、南方向をY軸、鉛直方向をZ軸とした座標系で指定する。
　　　(0, 0, 1) とすると、水平面内自動追従方式となる。

---

地　点 ：　　 月　日 ：　　 　
屋根傾斜角　：（度、0～90）　　 方　位　角　：（度、-180～180）

日射量単位： kWh/m2/日　　 MJ/m2/日
任意軸周り自動追従方式の回転軸（ベクトル指定）： 　

	太陽高度角、方位角、入射角のグラフ表示

　（注０） Erbs0: 固定方式、　Erbs1: 水平面内追従方式、　Erbs2: 完全追従方式、　Erbs3： 任意軸周り追従方式　の各斜面日射量。
　（注１） グラフ中の日射量の色は表中の色と対応する。
　（注２） 表中の全天、Erbs0～3の各文字をクリックすると個別にグラフ表示On/Off可能。
　（注３） 高度角、方位角、入射角は4時30分、5時30分、...、19時30分での値である。
　（注４） グラフでの太陽方位角は東：-90度、南：0度、西：+90度としている（再考(0)の計算式による値－180度）。

---

◆ 任意軸周り自動追従方式の計算式

　　● 座標系

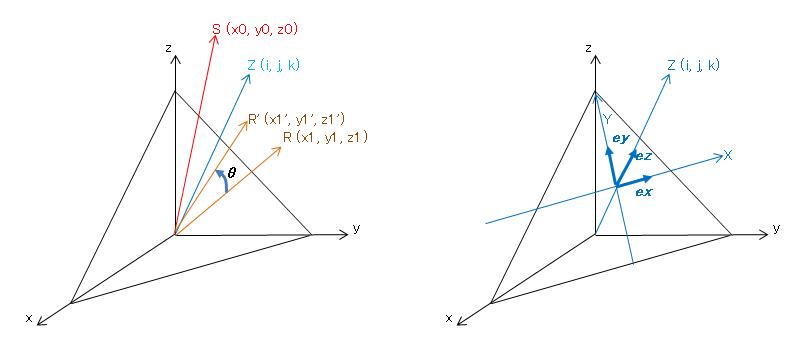
　基本座標系　原点：対象地点、x軸：西方向、y軸：南方向、z軸：鉛直方向とする直交座標系
　部分座標系　回転軸をZ軸とする座標系X-Y-Z
　

　　● 記号

　(i, j, k)　：　回転軸単位ベクトル
　(x0, y0, z0) ：　対象地点Oから太陽Sに向かう単位ベクトル
　(x1, y1, z1) ：　パネル面直単位ベクトル
　ex, ey, ez ：　回転軸をZ軸とする座標系X-Y-Zの各軸の方向ベクトル
　(X0, Y0, Z0)　：　(x0, y0, z0) のXYZ系での値
　(X1, Y1, Z1)　：　(x1, y1, z1) のXYZ系での値
　α　　：　太陽の高度角
　β　　：　太陽の方位角（南が0度、東が-90度、西が+90度）
　αr、βr：　屋根傾斜角と方位角
　θ　　：　日射量が最大となる回転角

　　● XYZ座標系の各軸方向ベクトル

　回転軸ベクトルに直交する平面がx軸、y軸と交わる点をPx, Pyとし、Px－＞Pyの方向にX軸をとる。
　　ex = (-j / √(i² + j²), i / √(i² + j²), 0)
　交点がない場合はx軸と同じ方向とする。　即ち、
　　ex = ( 1, 0, 0)
　Z軸とX軸からY軸を決める。
　　ez = (i, j, k)
　　ey = ez と ex の外積

　　● (X0, Y0, Z0) と (X1, Y1, Z1)

　　｜X0｜　　｜ex｜｜x0｜
　　｜Y0｜＝　｜ey｜｜y0｜
　　｜Z0｜　　｜ez｜｜z0｜

　　｜X1｜　　｜ex｜｜x1｜
　　｜Y1｜＝　｜ey｜｜y1｜
　　｜Z1｜　　｜ez｜｜z1｜

　　● (X1, Y1, Z1) を角θだけ回転したベクトル (X1', Y1', Z1')

　　｜X1'｜　　｜cosθ　-sinθ　0 ｜｜X1｜
　　｜Y1'｜＝　｜sinθ　 cosθ　0 ｜｜Y1｜
　　｜Z1'｜　　｜  0　     0 　 1 ｜｜Z1｜

　　● パネル面の日射強度Q： (X0, Y0, Z0) と (X1', Y1', Z1') の内積

　　Q = X0・X1' + Y0・Y1' + Z0・Z1'
　　  = X0・(X1cosθ - Y1sinθ) + Y0・(X1sinθ + Y1cosθ) + Z0・Z1'
　　  = (X0・X1 + Y0・Y1)cosθ + (Y0・X1 - X0・Y1)sinθ + Z0・Z1
　　　= a・cosθ + b・sinθ + c
　　　= √(a2+b2)・cos(θ-γ) + c
　ここで、
　　a = X0・X1 + Y0・Y1
　　b = Y0・X1 - X0・Y1
　　c = Z0・Z1
　　γ = atan(b/a)
　日射強度Qは θ＝γ で最大となり、その値は
　　Qmax = √(a2+b2) + c

　　● 日射強度Q最大となるときの (X1', Y1', Z1') と (x1', y1', z1')

　　｜X1'｜　　｜cosθ　-sinθ　0 ｜｜X1｜
　　｜Y1'｜＝　｜sinθ　 cosθ　0 ｜｜Y1｜
　　｜Z1'｜　　｜  0　     0 　 1 ｜｜Z1｜

　　｜x1'｜　　｜exx eyx ezx｜｜X1'｜　　（注）ex = (exx, exy, exz) など
　　｜y1'｜＝　｜exy eyy ezy｜｜Y1'｜
　　｜z1'｜　　｜exz eyz ezz｜｜Z1'｜

　　● 日射強度Q最大となるときのパネル（屋根）の傾斜角αrと方位角βr

　　αr = acos(z1')
　　βr = 90 - atan(y1'/x1')