■ ゴルフの賞金分配率(2a): 1 + 1/2 + 1/3 + ・・・+ 1/n の近似値(JavaScript版)
毎年、年末が近づくと男子・女子ともゴルフの賞金王争いが話題になります。
一般に男子では優勝賞金は賞金総額の20%、女子では18%となっており、2位以下は順次低減していきます。
順位と賞金の分配率の関係は実際には主催団体、大会毎に決められるようですが、どのような計算式に基づいているのでしょうか。
ゴルフの賞金分配率(1a)にもあるように、分配率 y は順位 x にほぼ反比例する、すなわち
y = y1 / x
として、概略の配分を速算することができます(y1:優勝者 = 1位の分配率)。
2位は1位の約1/2 (1位が20%なら、10%)
10位は1位の約1/10 (1位が20%なら、 2%)
50位は1位の約1/50 (1位が20%なら、 0.4%)
従って、1位~n位までの賞金累積値(概略値)は
y1 ( 1 + 1/2 + 1/3 + ・・・+ 1/n )
となります。
国内男子ツアーの場合、通常は予選上位60位までが決勝ラウンドに進みます。
●調和級数: 1 + 1/2 + 1/3 + ・・・+ 1/n の近似値
 さて、ここでは分配率の累積値に関連して、調和級数:
さて、ここでは分配率の累積値に関連して、調和級数:
1 + 1/2 + 1/3 + ・・・+ 1/n
の値の近似式を考えてみましょう。
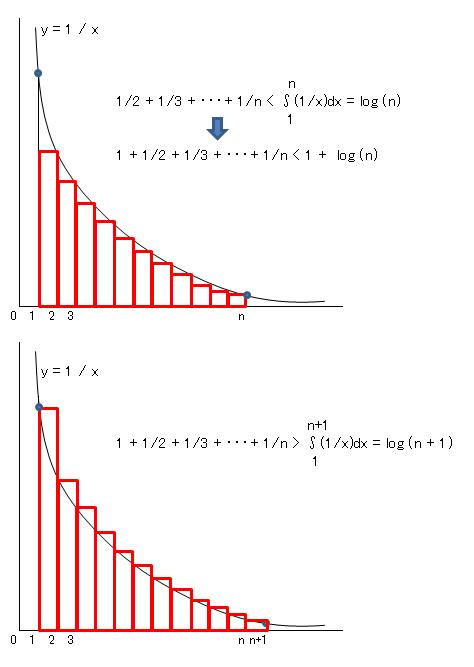
関数 y = 1 / x の定積分: (注)log (n) は自然対数を表す。
∫1n (1 / x) dx = log (n)
∫1n+1 (1 / x) dx = log (n+1)
と そのグラフから、以下の式が成立します。
log (1+n) < 1 + 1/2 + 1/3 + ・・・+ 1/n < 1 + log (n) ・・・(式 0)
これから、以下の近似式が得られます。
・(近似式1)
(式 0)の左右の式の平均値として
1 + 1/2 + 1/3 + ・・・+ 1/n ≒ [ 1 + log (n) + log (n+1) ] / 2 ・・・(式 1)
・(近似式2)
(式 0)から log (n) を引くと
log (n+1) - log (n) < 1 + 1/2 + 1/3 + ・・・+ 1/n - log (n) < 1
log (1 + 1/n) < 1 + 1/2 + 1/3 + ・・・+ 1/n - log (n) < 1
ここで、 n→∞ の極限を取ると、
0 ≦ lim [ 1 + 1/2 + 1/3 + ・・・+ 1/n - log (n) ] ≦ 1
n→∞
となり、
γ=lim [ 1 + 1/2 + 1/3 + ・・・+ 1/n - log (n) ]
n→∞
が0~1の間の有限の値に収束することがわかります。
この極限値 γ はオイラー(Euler)の定数と呼ばれ、
γ= 0.5772156649…
従って、nが大きい時、
1 + 1/2 + 1/3 + ・・・+ 1/n ≒ log (n) + γ ・・・(式 2)
下図のアプリは調和級数の真の値と上記近似式による値を比較したものです。
項数 n≧6において、(式 1)より(式 2)の方が近似度がいいことがわかります。
右側の表ではn=1000までの値を表示できます。
(式 2)と(式 1)の値の差は
log (n) + γ - [ 1 + log (n) + log (n+1) ] / 2
= γ- 1/2 - [ log (n+1) - log (n) ] / 2
= γ- 1/2 - [ log (1 + 1/n) ] / 2
であり、項数 nの増加とともに次第に一定値(γ - 0.5 = 0.0772...)に近づきます。
[参考文献] Wikipedia: オイラーの定数、調和級数
ホーム
 さて、ここでは分配率の累積値に関連して、調和級数:
さて、ここでは分配率の累積値に関連して、調和級数: