■ 球面と２つの回転楕円体の交点を求める （JavaScript版）

　球面：
　　中心 P1(x1, y1, z1)、　半径 r1 の球面１
と次の２曲面：
　　球中心P1と点P2(x2, y2, z2)からの距離の和が等しい点の集合が作る曲面２
　　球中心P1と点P3(x3, y3, z3)からの距離の和が等しい点の集合が作る曲面３
の交点について検討します。

　２点からの距離の和が等しい点の集合は回転楕円体ですので、球面と２つの回転楕円体の交点に関する話題です。

　球面１と回転楕円体２の交線は（もしあるとすれば）円です。　同様に、球面１と回転楕円体３の交線も円です。
　これら２つの交線（円）が図のような状態にあれば、球面と２つの回転楕円体が交わる（共有点を持つ）ことになります。

　

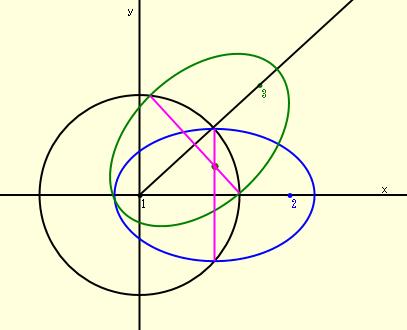
　ここでは、これに関する計算式を示すとともに、確認のための簡単なアプリを作成しました。

　・球面の中心P1を座標原点、点P2方向にｘ軸、
　　3点 P1、P2、P3を通る平面の法線ベクトル方向にｚ軸、
　　ｘｙｚ座標系が右手直交座標系になるようにｙ軸をとります。
　・次の値を入力します。
　　　・球面の半径 r
　　　・P2 のｘ座標（＞ 0）
　　　・P3 のｘ、ｙ座標
　・各楕円体について、２点からの距離の和 を指定します。
　・「計算」ボタンをクリックすると、計算結果（交点）を表示します。

球No.xcyczc半径 r
1:
点No.xyzP1からの距離の和
2: （P1-P-P2）
3: （P1-P-P3）



●画面操作方法 
・マウスホイールで表示図形の拡大縮小が可能。
・a2/b2、a3/b3 は回転楕円体の係数。
・px, py, pz は交点座標。
●球面と回転楕円体の交線の求め方 
　球面１の中心を原点(0, 0, 0)とし、点P2はX軸上の(x2, 0, 0)にあるものとします。

　球面１の式：
　　x2 + y2 + z2 = r12　・・・（式1.1）

　回転楕円体の式：
　　( x - e )2/a2 + ( y2 + z2 )/b2 = 1　・・・（式1.2）
　　ここで、
　　　x2 < L
　　　e = x2/2
　　　a = L/2  ( L は中心P1、P2からの距離の和)
　　　b = ( a2 - e2 )1/2

　(式1.2)の両辺に b2を乗ずると、
　　( x - e )2(b/a)2 + y2 + z2 = b2　・・・（式1.2'）

　(式1.1)から(式1.2')を引くと、y, zが消去され、x に関する次の2次方程式が得られます。
　　Ax2 + Bx + C = 0
　　ここで、
　　　A = a2 - b2
　　　B = 2b2e
　　　C = -(be)2 - a2(r12 - b2 )

　これより、交線である円のｘ座標が得られます。

　球面１と回転楕円体３の交線もP1P2方向をX軸とする局所座標系で考えれば上と同様に求められます。
　計算後、全体座標系での値に戻します。
●球面と２つの回転楕円体の交点の求め方 
　上で得られた2つの交線（円）の交点が求める交点になります。
　図の座標系で示す2本のピンクの交線（線分）の交点の求め方は以下のとおり。

　球面１と回転楕円体２の交線を示す線分L12の両端点をQ2a(x2a, y2a), Q2b(x2b, y2b)、
　球面１と回転楕円体３の交線を示す線分L13の両端点をQ3a(x3a, y3a), Q3b(x3b, y3b)
　とし、両線分をパラメータ s,　t を用いて表すと、
　　L12：　P = Q2a・(1-s) + Q2b・s　　（0≦s≦1）
　　L13：　P = Q3a・(1-t) + Q3b・t　　（0≦t≦1）

　これより、交点では
　　Q2a・(1-s) + Q2b・s = Q3a・(1-t) + Q3b・t

　x座標、y座標で表現すると、
　　x2a・(1-s) + x2b・s = x3a・(1-t) + x3b・t
　　y2a・(1-s) + y2b・s = y3a・(1-t) + y3b・t

　この連立方程式を解いて s, tを求め、0≦s≦1、0≦t≦1 であれば交点があります。
　交点座標Pcは
　　Pc = Q2a・(1-s) + Q2b・s
ホーム