中心 P1(x1, y1, z1) 半径 r1 の球面1
中心 P2(x2, y2, z2) 半径 r2 の球面2
の中心P1、P2からの距離の和が等しい点の集合は回転楕円体です。
これら2球面と回転楕円体の交点について検討します。
2球面の交線は円であり、上記回転楕円体がこれと交わる(接する)のは図の赤線の状態です。
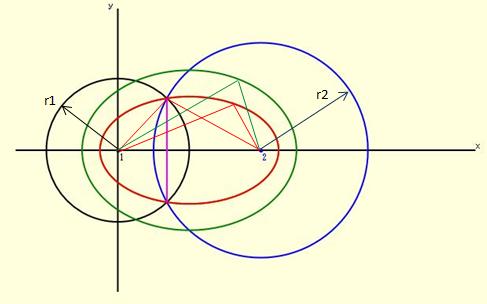
ここでは、これに関する計算式を示すとともに、確認のための簡単なアプリを作成しました。
・2球面の中心座標(xc, yc, zc)、半径 r を入力します。
球面1の中心P1は(0, 0, 0)で固定とします。
球面2の中心P2はX軸上にあり、(x2, 0, 0)とします(x2 > 0)。
・2点からの距離の和 を指定します(最小、最大、分割数)。
・「計算」ボタンをクリックすると、計算結果(交点)を表示します。
赤線が2球面と回転楕円体が接する場合、緑色が指定された距離の和に対するものです。
画面右上部の a、b 値は楕円体の式(下記)における値です。
●画面操作方法
・マウスホイールで表示図形の拡大縮小が可能。 ・画面上をクリックすると、その点を通る回転楕円体とa,b 値を表示します(水色)。●2球面と回転楕円体の交線の求め方
球面1の中心を原点(0, 0, 0)とし、球面2の中心はX軸上の(x2, 0, 0)にあるものとします。 回転楕円体の式: ( x - e )2/a2 + ( y2 + z2 )/b2 = 1 ここで、 e = x2/2 a = L/2 ( L は中心P1、P2からの距離の和) b = ( a2 - e2 )1/2 2球面の交線である円に対して、回転楕円体が交わる(接する)のは、 L = r1 + r2 のときです。