自己交差を持たない多角形の面積を座標法により求める際の計算式について記しています。
多角形の頂点を(X1,Y1), (X2,Y2), ..., (Xn,Yn)とする。
このとき、自己交差を持たない多角形の面積 S は下記式で与えられる。
(1)S = (1/2)|Σ[XiYi+1 - Xi+1Yi]|
(2)S = (1/2)|Σ[(Xi - Xi+1)(Yi + Yi+1)]|
(3)S = (1/2)|Σ[Xi(Yi+1 - Yi-1]|
(4)S = (1/2)|Σ[(Xi+1 - Xi-1)Yi]|
ここで、
Σ: i=1, 2, ..., n についての総和
Xn+1 = X1, X0 = Xn
Yn+1 = Y1, Y0 = Yn
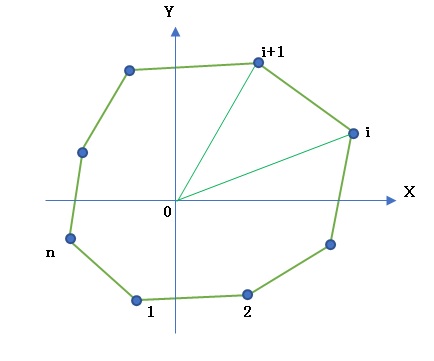 Fig.1
以下に、これらの式の導出方法の1例について簡単に記す。
(1)S = (1/2)|Σ[XiYi+1 - Xi+1Yi]|
原点0と頂点i、i+1 からなる3角形の面積 Siは、ベクトル 0ー>i、0->i+1の外積:
| i j k | (注)1行目のi、j、kはXYZ軸方向の単位ベクトル
| Xi Yi 0 |
| Xi+1 Yi+1 0 |
のZ成分の1/2 であるから、
Si = (1/2)[XiYi+1 - Xi+1Yi]
多角形の面積 Sはこれらの和である(点列の向きが時計回りのときは負になるので絶対値をとる)。
下図 Fig.1aのような頂点配列の場合、△0~i~i+1の面積 Si> 0である。
△0~i+1~i+2の面積は負、△0~i+2~i+3の面積は正で、これら2つの面積の和は0~i+1~i+2~i+3からなる4辺形の面積となる。
従って、このような場合に対しても前掲のSiの和が多角形の面積となる。
Fig.1
以下に、これらの式の導出方法の1例について簡単に記す。
(1)S = (1/2)|Σ[XiYi+1 - Xi+1Yi]|
原点0と頂点i、i+1 からなる3角形の面積 Siは、ベクトル 0ー>i、0->i+1の外積:
| i j k | (注)1行目のi、j、kはXYZ軸方向の単位ベクトル
| Xi Yi 0 |
| Xi+1 Yi+1 0 |
のZ成分の1/2 であるから、
Si = (1/2)[XiYi+1 - Xi+1Yi]
多角形の面積 Sはこれらの和である(点列の向きが時計回りのときは負になるので絶対値をとる)。
下図 Fig.1aのような頂点配列の場合、△0~i~i+1の面積 Si> 0である。
△0~i+1~i+2の面積は負、△0~i+2~i+3の面積は正で、これら2つの面積の和は0~i+1~i+2~i+3からなる4辺形の面積となる。
従って、このような場合に対しても前掲のSiの和が多角形の面積となる。
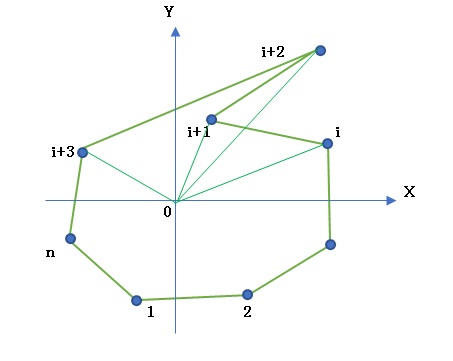 Fig.1a
また、座標原点0が多角形の外部にあるときを考える(Fig.1b)。
多角形の内部に点C(x0,y0)をとると、三角形C~i~i+1の面積Aiは
Ai = (1/2)[(Xi-x0)(Yi+1-y0) - (Xi+1-x0)(Yi-y0)]
変形すると、
Ai = (1/2)[XiYi+1 - Xi+1Yi]
+ (1/2)[Yi - Yi+1]x0
+ (1/2)[Xi+1 - Xi]y0
多角形の面積はこれをi=1~nについて合計すればよいが、例えば[Yi - Yi+1]などについては、
Y1-Y2 + Y2-Y3 + ・・・ + Y(n-1)-Yn + Yn - Y1 = 0
となるから、Aiの合計はSiの合計と等しくなる。
Fig.1a
また、座標原点0が多角形の外部にあるときを考える(Fig.1b)。
多角形の内部に点C(x0,y0)をとると、三角形C~i~i+1の面積Aiは
Ai = (1/2)[(Xi-x0)(Yi+1-y0) - (Xi+1-x0)(Yi-y0)]
変形すると、
Ai = (1/2)[XiYi+1 - Xi+1Yi]
+ (1/2)[Yi - Yi+1]x0
+ (1/2)[Xi+1 - Xi]y0
多角形の面積はこれをi=1~nについて合計すればよいが、例えば[Yi - Yi+1]などについては、
Y1-Y2 + Y2-Y3 + ・・・ + Y(n-1)-Yn + Yn - Y1 = 0
となるから、Aiの合計はSiの合計と等しくなる。
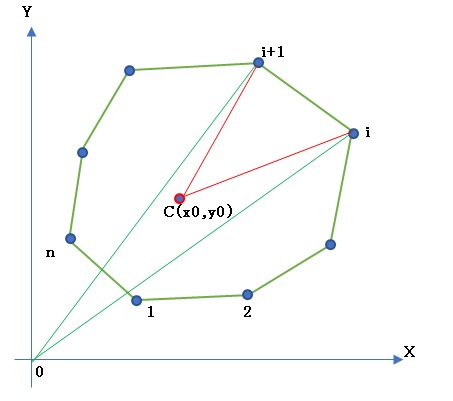 Fig.1b
(2)S = (1/2)|Σ[(Xi - Xi+1)(Yi + Yi+1)]|
頂点i、i+1からX軸上に下した垂線の足をi'、i+1'とすると、これら4点で構成される台形の面積 Siは
Si = (1/2)[(Xi - Xi+1)(Yi + Yi+1)]
多角形の面積 Sはこれらの和である。
Fig.1b
(2)S = (1/2)|Σ[(Xi - Xi+1)(Yi + Yi+1)]|
頂点i、i+1からX軸上に下した垂線の足をi'、i+1'とすると、これら4点で構成される台形の面積 Siは
Si = (1/2)[(Xi - Xi+1)(Yi + Yi+1)]
多角形の面積 Sはこれらの和である。
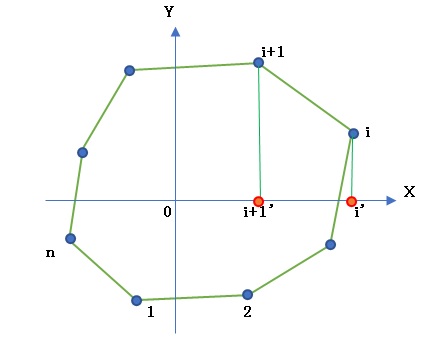 Fig.2
(3)S = (1/2)|Σ[Xi(Yi+1 - Yi-1]|
式(2)で、Xiの係数を拾い集めると、 (注)(1/2)はひとまず置いておく
Yi + Yi+1
-(Yi-1 + Yi)
= Yi+1 - Yi-1
従って、多角形の面積 SはこれにXiを乗じたものの和の(1/2)となる。
(4)S = (1/2)|Σ[(Xi+1 - Xi-1)Yi]|
(3)と同様な方法で導き出せる(省略)。
Fig.2
(3)S = (1/2)|Σ[Xi(Yi+1 - Yi-1]|
式(2)で、Xiの係数を拾い集めると、 (注)(1/2)はひとまず置いておく
Yi + Yi+1
-(Yi-1 + Yi)
= Yi+1 - Yi-1
従って、多角形の面積 SはこれにXiを乗じたものの和の(1/2)となる。
(4)S = (1/2)|Σ[(Xi+1 - Xi-1)Yi]|
(3)と同様な方法で導き出せる(省略)。
Fig.1 以下に、これらの式の導出方法の1例について簡単に記す。 (1)S = (1/2)|Σ[XiYi+1 - Xi+1Yi]| 原点0と頂点i、i+1 からなる3角形の面積 Siは、ベクトル 0ー>i、0->i+1の外積: | i j k | (注)1行目のi、j、kはXYZ軸方向の単位ベクトル | Xi Yi 0 | | Xi+1 Yi+1 0 | のZ成分の1/2 であるから、 Si = (1/2)[XiYi+1 - Xi+1Yi] 多角形の面積 Sはこれらの和である(点列の向きが時計回りのときは負になるので絶対値をとる)。 下図 Fig.1aのような頂点配列の場合、△0~i~i+1の面積 Si> 0である。 △0~i+1~i+2の面積は負、△0~i+2~i+3の面積は正で、これら2つの面積の和は0~i+1~i+2~i+3からなる4辺形の面積となる。 従って、このような場合に対しても前掲のSiの和が多角形の面積となる。
Fig.1a また、座標原点0が多角形の外部にあるときを考える(Fig.1b)。 多角形の内部に点C(x0,y0)をとると、三角形C~i~i+1の面積Aiは Ai = (1/2)[(Xi-x0)(Yi+1-y0) - (Xi+1-x0)(Yi-y0)] 変形すると、 Ai = (1/2)[XiYi+1 - Xi+1Yi] + (1/2)[Yi - Yi+1]x0 + (1/2)[Xi+1 - Xi]y0 多角形の面積はこれをi=1~nについて合計すればよいが、例えば[Yi - Yi+1]などについては、 Y1-Y2 + Y2-Y3 + ・・・ + Y(n-1)-Yn + Yn - Y1 = 0 となるから、Aiの合計はSiの合計と等しくなる。
Fig.1b (2)S = (1/2)|Σ[(Xi - Xi+1)(Yi + Yi+1)]| 頂点i、i+1からX軸上に下した垂線の足をi'、i+1'とすると、これら4点で構成される台形の面積 Siは Si = (1/2)[(Xi - Xi+1)(Yi + Yi+1)] 多角形の面積 Sはこれらの和である。
Fig.2 (3)S = (1/2)|Σ[Xi(Yi+1 - Yi-1]| 式(2)で、Xiの係数を拾い集めると、 (注)(1/2)はひとまず置いておく Yi + Yi+1 -(Yi-1 + Yi) = Yi+1 - Yi-1 従って、多角形の面積 SはこれにXiを乗じたものの和の(1/2)となる。 (4)S = (1/2)|Σ[(Xi+1 - Xi-1)Yi]| (3)と同様な方法で導き出せる(省略)。